|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
Implementation details for Brusselator_scheme::prePattern_loop(). More...
#include <brusselator_algo_impl.h>
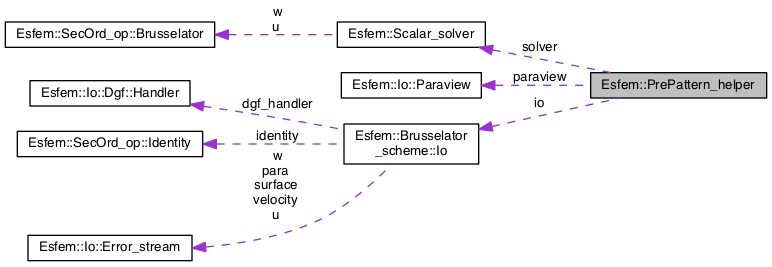
Public Member Functions | |
| PrePattern_helper (Brusselator_scheme &) | |
Modifies private data members of Brusselator_scheme | |
| void | rhs () |
Adds to member rhs_les from Brusselator_scheme::fef.u and Brusselator_scheme::fef.w More... | |
| void | solve_pde () |
New value for member fun from Brusselator_scheme::fef.u and Brusselator_scheme::fef.w More... | |
| void | prepare_rhs () |
New value for member rhs_les from Brusselator_scheme::fef.u and Brusselator_scheme::fef.w More... | |
| void | plot_paraview () |
Prints out fun of Brusselator_scheme::fef.u and Brusselator_scheme::fef.w. | |
Private Attributes | |
| Brusselator_scheme::Io & | io |
Reference to Brusselator_scheme::io | |
| Grid::Scal_FEfun_set & | u |
Reference to Brusselator_scheme::fef.u | |
| Grid::Scal_FEfun_set & | w |
Reference to Brusselator_scheme::fef.w | |
| const Dune::Fem::TimeProviderBase & | tp |
| Io::Paraview | paraview |
Has reference to member fun from u and w | |
| Scalar_solver | solver |
| Brusselator solver. | |
Implementation details for Brusselator_scheme::prePattern_loop().
Definition at line 108 of file brusselator_algo_impl.h.
| void PrePattern_helper::prepare_rhs | ( | ) |
New value for member rhs_les from Brusselator_scheme::fef.u and Brusselator_scheme::fef.w
rhs_les will have the following value for 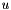 respectively
respectively 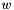 :
:
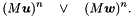
Definition at line 135 of file brusselator_algo_impl.cpp.
| void PrePattern_helper::rhs | ( | ) |
Adds to member rhs_les from Brusselator_scheme::fef.u and Brusselator_scheme::fef.w
The new value of rhs_les from Brusselator_scheme::fef.u respectively Brusselator_scheme::fef.w will be
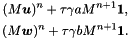
Note that the surface is not changing at this stage.
Definition at line 123 of file brusselator_algo_impl.cpp.
| void PrePattern_helper::solve_pde | ( | ) |
New value for member fun from Brusselator_scheme::fef.u and Brusselator_scheme::fef.w
We assume that the rhs_les has been prepared with finalize_rhs(). The vaule of fun will be overwritten with the solution of the following system for 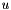 and
and 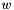 :
:
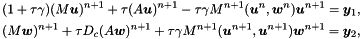
where 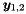 the right-hand side of the system is.
the right-hand side of the system is.
Definition at line 129 of file brusselator_algo_impl.cpp.
|
private |
From Brusselator_scheme::fix_grid
Definition at line 167 of file brusselator_algo_impl.h.
 1.8.10
1.8.10