|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
Implementation of the Elliott and Styles full discretization of the tumor problem. More...
#include <brusselator_algo.h>
Classes | |
| struct | Fef |
| Shortens Brusselator_scheme(). More... | |
| struct | Init_data |
| Initial data respectively exact solution for numerical experiments. More... | |
| struct | Io |
| Shortens Brusselator_scheme(). More... | |
Public Member Functions | |
| Brusselator_scheme (int argc, char **argv, const std::string ¶meter_fname) | |
| The constructor that also performs the first part before the loop enters. More... | |
| void | eoc_logisticSphere () |
| Experiment, where right-hand side is calculated for a known solution. More... | |
| void | eoc_mcf () |
| Dziuk mean curvature flow ESFEM. More... | |
| void | sd () |
| Sphere Dalquist. More... | |
| void | eoc_sls () |
| Surface logistic sphere. More... | |
| void | eoc_sdp () |
| EOC experiment for solution driven paper. More... | |
| void | test () |
| Run a simple test. | |
Prescribed ESFEM | |
| void | standard_esfem () |
| Standard Dziuk Elliott evolving surface finite element method. | |
Loop action | |
| void | prePattern_loop () |
In some sense calculates the inital data for the solution driven problem. Starts from  . . | |
| void | intermediate_action () |
| To be used between prePattern_loop() and pattern_loop(). More... | |
| void | pattern_loop () |
To be used in the second for-loop. If prePattern_loop() is off, then  is here. More... is here. More... | |
| void | final_action () |
| To be used after the second for-loop to save some data. | |
Private Member Functions | |
| void | update_surface () |
Assign a new value to fef.surface.exact and fef.surface.app | |
| void | update_scalar_solution () |
Assign a new value to fef.u.exact and fef.w.exact | |
| template<class F > | |
| void | print (Esfem::Io::Error_stream &os, const F &fem) |
| Lifted printing. | |
| template<class It1 , class It2 > | |
| void | calculate_velocity (It1 xn_first, It1 xn_last, It1 xo_first, It2 v_first) |
| Calculate the velocity via simple differential quotient. More... | |
| void | error_on_intSurface () |
Plot error of fef on the interpolated surface. More... | |
| void | pre_loop_action () |
| Constructor helper. More... | |
| void | rhs_and_solve_SPDE () |
| Helper for pattern_loop(). More... | |
Flow control | |
| void | next_timeStep () |
Increments the next time step in fix_grid. | |
| long | prePattern_timeSteps () const |
| Maximum number of time steps for prePattern_loop(). | |
| long | pattern_timeSteps () const |
| Maximum number of time steps for pattern_loop(). | |
| long | time_steps () const |
| Absolute number of time steps. | |
Private Attributes | |
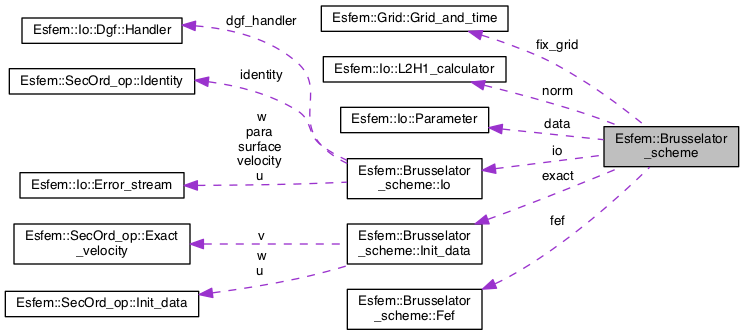
| Esfem::Io::Parameter | data |
Contains parameter from tumor_parameter.txt. | |
| Io | io |
| Error streams and identity functor for the surface. | |
| Esfem::Grid::Grid_and_time | fix_grid |
| Analytically given grid with absolute time provider. | |
| Esfem::Io::L2H1_calculator | norm |
| Norms on the analytically given grid. | |
| Fef | fef |
| Finite element functions. | |
| Init_data | exact |
Exact solution for  , , 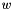 and and 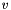 . . | |
Friends | |
Helper classes for the for-loops | |
| class | PreLoop_helper |
| Used in pre_loop_action(). | |
| class | PrePattern_helper |
| Used in prePattern_loop(). | |
| class | Pattern_helper |
| Used in pattern_loop(). | |
| class | RhsAndSolve_helper |
| Used in rhs_and_solve_SPDE(). | |
Implementation of the Elliott and Styles full discretization of the tumor problem.
 for the scalar equation with
for the scalar equation with 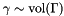 .
. for the surface equation, where
for the surface equation, where 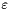 and
and 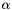 are small regularization parameter.
are small regularization parameter.Find  (growth-promoting),
(growth-promoting),  (growth-inhibiting) and
(growth-inhibiting) and ![$X\colon \surface_{0} \times [0,T] \to \R^{m+1}$](form_13.png) such that
such that
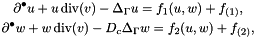
where for 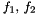 we use the Brusselator model
we use the Brusselator model
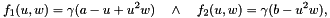
and 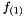 and
and 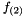 are some forcing terms, and for the surface
are some forcing terms, and for the surface
![\begin{align*} v - \alpha \laplaceBeltrami v = {} & \parentheses[\big]{\varepsilon (-\meanCurvature) + \delta u} \surfaceNormal + g = \varepsilon \laplaceBeltrami X + \delta u \surfaceNormal + g, \\ \dell_{t} X = {} & v(X), \end{align*}](form_111.png)
where 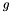 is a forcing term.
is a forcing term.
Find  (growth-promoting nodal values),
(growth-promoting nodal values),  (growth-inhibiting nodal values) and
(growth-inhibiting nodal values) and  (surface nodal values) such that
(surface nodal values) such that
![\begin{gather*} \parentheses[\big]{M(X) + \alpha A(X)} \dell_t X = -\varepsilon A(X)X + \delta M(u,\nodalValue{\surfaceNormal}) + G, \\ \dell_t \parentheses[\big]{M(X) \nodalValue{u} } + A(X) \nodalValue{u} = \gamma \parentheses[\big]{a M(X) \nodalValue{1} - M(X)\nodalValue{u} + M(X; \nodalValue{u},\nodalValue{w}) \nodalValue{u}} + F_{(1)} \\ \dell_t \parentheses[\big]{M(X) \nodalValue{w}} + D_c A(X) \nodalValue{w} = \gamma \parentheses[\big]{b M(X) \nodalValue{1} - M(X; \nodalValue{u},\nodalValue{u}) \nodalValue{w}} + F_{(2)}. \end{gather*}](form_112.png)
We note that instead of the 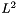 -projection we use the interpolation of
-projection we use the interpolation of 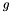 ,
, 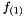 respectively
respectively 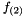 .
.
We perform three steps.
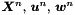 solve for
solve for 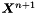
![\begin{equation*} \parentheses[\big]{M_3^n + (\alpha + \varepsilon\tau) A_3^n} \nodalValue{X}^{n+1} = (M_3^n + \alpha A_3^n) \nodalValue{X}^n + \tau \delta M_3^n(\nodalValue{u}^n, \nodalValue{\surfaceNormal}) + \tau G^n, \end{equation*}](form_46.png)
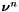 is elementwise normal.
is elementwise normal.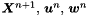 solve for
solve for 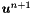
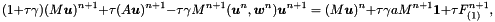
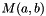 a
a 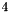 tensor is, namely
tensor is, namely 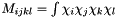 and
and 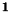 means the constant
means the constant 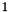 finite element function.
finite element function.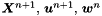 solve for
solve for 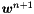
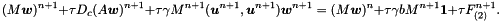
Definition at line 147 of file brusselator_algo.h.
| Brusselator_scheme::Brusselator_scheme | ( | int | argc, |
| char ** | argv, | ||
| const std::string & | parameter_fname | ||
| ) |
The constructor that also performs the first part before the loop enters.
| argc | argc from main | |
| [in] | argv | argv from main |
| parameter_fname | Preferable absolute path to parameter file. |
Definition at line 71 of file brusselator_algo.cpp.
|
inlineprivate |
Calculate the velocity via simple differential quotient.
| [in] | xn_first | Iterator to first point of the new surface |
| [in] | xn_last | Iterator to last point of the new surface |
| [in] | xo_first | Iterator to first point of the previous surface |
| [out] | v_first | Iterator to the first value of the velocity |
xo_first and v_first point to as many elements as xn_first does. Definition at line 438 of file brusselator_algo.h.
| void Brusselator_scheme::eoc_logisticSphere | ( | ) |
Experiment, where right-hand side is calculated for a known solution.
As exact solution for the scalar valued surface equation I chose
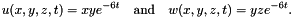
For the surface evolution I chose
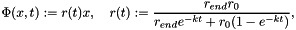
where 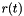 is the logistic growth function, which satisfies the following ODE
is the logistic growth function, which satisfies the following ODE
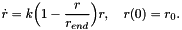
From this it follows easily that the velocity is given by
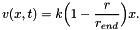
Definition at line 116 of file brusselator_algo.cpp.
| void Brusselator_scheme::eoc_mcf | ( | ) |
Dziuk mean curvature flow ESFEM.
(This is not any more true) Experiment reads as follows: Stationary surface  with exact solution
with exact solution  , with the formula
, with the formula
![\[ \Delta f = \Delta_{\R^{n+1}} f - H D_{\R^{n+1}} f \cdot n - D^2_{\R^{n+1}} f(n,n), \]](form_136.png)
and
![\[ H = div(n) = \frac{n}{|x|} \]](form_137.png)
one easily sees
![\[ \Delta(xy) = -\frac{2n+2}{|x|^2} xy, \]](form_138.png)
which implies that the right-hand side of the surface PDE vanishes.
Definition at line 169 of file brusselator_algo.cpp.
| void Brusselator_scheme::eoc_sdp | ( | ) |
EOC experiment for solution driven paper.
As exact solution for the surface evolution I choose
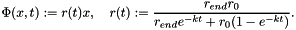
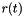 satiesfies the ODE
satiesfies the ODE
![\[ \dot{r}(t) = k \left( 1 - \frac{r(t)}{r_{end}}\right) r(t), \]](form_169.png)
which implies for the velocity
![\[ v(x,t) = k \left( 1 - \frac{r(t)}{r_{end}} \right)x =: \tilde{a} x \]](form_170.png)
As exact solution for the scalar diffusion equation I choose
![\[ u(x,t) := x_1 x_2 e^{-6t}. \]](form_175.png)
The coupled PDE equations reads as
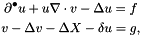
where  is given via
is given via
![\[ g = \left( \tilde{a} + \frac{(\alpha \tilde{a} + \varepsilon)H - \delta u}{|x|}\right) x, \]](form_180.png)
and the complicated 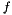 is computed via Sage.
is computed via Sage.
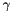 has to be zero.
has to be zero. Definition at line 242 of file brusselator_algo.cpp.
| void Brusselator_scheme::eoc_sls | ( | ) |
Surface logistic sphere.
As exact solution for the surface evolution I choose
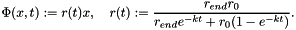
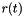 satiesfies the ODE
satiesfies the ODE
![\[ \dot{r}(t) = k \left( 1 - \frac{r(t)}{r_{end}}\right) r(t), \]](form_169.png)
which implies for the velocity
![\[ v(x,t) = k \left( 1 - \frac{r(t)}{r_{end}} \right)x =: \tilde{a} x \]](form_170.png)
I do not consider coupling. For the surface PDE I choose
![\[ v - \alpha \Delta v - \varepsilon \Delta x - \delta u \vec{n} = f, \]](form_173.png)
where 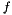 must be
must be
![\[ f = \left( \tilde{a} + \frac{(\alpha \tilde{a} + \varepsilon)H - \delta u}{|x|}\right) x, \]](form_174.png)
where we have used  , where
, where 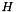 is the mean curvature (without aritmetic mean) and
is the mean curvature (without aritmetic mean) and 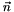 is the outwards pointing normal, and
is the outwards pointing normal, and 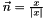 . It holds
. It holds 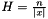 , where
, where 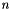 is the dimension of the sphere. Note that
is the dimension of the sphere. Note that 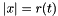 on the exact surface.
on the exact surface.
Definition at line 191 of file brusselator_algo.cpp.
|
private |
Plot error of fef on the interpolated surface.
Definition at line 370 of file brusselator_algo.cpp.
| void Brusselator_scheme::intermediate_action | ( | ) |
To be used between prePattern_loop() and pattern_loop().
The inital data has been created. It will be saved and the right hand side for the surface PDE will be created.
Definition at line 301 of file brusselator_algo.cpp.
| void Brusselator_scheme::pattern_loop | ( | ) |
To be used in the second for-loop. If prePattern_loop() is off, then 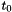 is here.
is here.
At this stage the tumor is growing.
Definition at line 314 of file brusselator_algo.cpp.
|
private |
Constructor helper.
Definition at line 393 of file brusselator_algo.cpp.
|
private |
Helper for pattern_loop().
Generates first part of the right-hand side for the scalar SPDE. Then solves the vector SPDE and prints out a dgf file.
Definition at line 406 of file brusselator_algo.cpp.
| void Brusselator_scheme::sd | ( | ) |
Sphere Dalquist.
Initial surface is unit sphere in  . Exact solution is
. Exact solution is
![\[ \Phi(x,t) := r(t)x,\quad r(t):= e^t \]](form_167.png)
The PDE is
![\[ v - \alpha \Delta v - \varepsilon \Delta x = f(x,t) = (1 + (\alpha + \varepsilon) 2 e^{-2t})x. \]](form_171.png)
Definition at line 220 of file brusselator_algo.cpp.
 1.8.10
1.8.10