|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
Vector valued right-hand side for the mean curvature equation. More...
#include <secOrd_op_rhs_impl.h>


Public Types | |
| using | Base = Esfem::Grid::Grid_and_time::Vec_Function_space |
| Template argument. | |
| using | Domain = Base::DomainType |
 | |
| using | Range = Base::RangeType |
 | |
Public Member Functions | |
| Vec_rhs_fun (const Dune::Fem::TimeProviderBase &) | |
| Get time and time step. More... | |
| Vec_rhs_fun (const Vec_rhs_fun &)=delete | |
| No copy construct. | |
| Vec_rhs_fun & | operator= (const Vec_rhs_fun &)=delete |
| No copy assignment. | |
| void | evaluate (const Domain &, Range &) const |
| y = f(x) | |
| Range | operator() (const Domain &) const |
| y = f(x) | |
Private Member Functions | |
| void | update_cache () const |
Conditional update member cache More... | |
Private Attributes | |
| const Dune::Fem::TimeProviderBase & | tp |
| Time and time step. | |
| double | alpha |
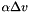 | |
| double | epsilon |
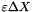 | |
| double | r_start |
| Initial size of sphere. | |
| double | r_end |
| Final size of sphere. | |
| double | k |
| Steepness of logistic growh. | |
| double | delta |
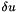 | |
| double | cache [4] |
| Helper variable, which save computations. | |
Vector valued right-hand side for the mean curvature equation.
This is my right-hand function:
![\[ \biggl[ k \Bigl( 1 - \frac{r(t)}{r_{end}}\Bigr) \lvert X \rvert + 2 \Bigl(\alpha k \Bigl( 1 - \frac{r(t)}{r_{end}}\Bigr) + \varepsilon \Bigr) \frac{1}{\lvert X \rvert} - \delta xy e^{-6t}\biggr] \]](form_113.png)
Currently I am testing. So, I use an easier right-hand side. I am doing classic mean curvature flow on the sphere. Right-hand side must be zero for this example. Also I expect unit sphere as starting value, alpha = 0 and epsilon = 1.
Old test, which I want to check again later:
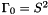
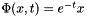
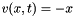
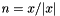
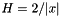
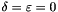 , hence the operator is
, hence the operator is
![\[ v - \alpha \Delta v = g(x,t) = -(1 + \alpha 2/ |x|^2) x. \]](form_132.png)
Definition at line 97 of file secOrd_op_rhs_impl.h.
|
explicit |
Get time and time step.
this, then you are in problem. Definition at line 103 of file secOrd_op_rhs_impl.cpp.
|
private |
Conditional update member cache
cache[0] holds the last time. If the current time does not equals cache[0], then update the cache. The content of cache is
cache[0] = tp.time(),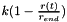 ,
,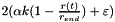 ,
,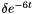 ,
,where 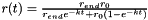
Definition at line 117 of file secOrd_op_rhs_impl.cpp.
 1.8.10
1.8.10