|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
Solve the surface partial differential equation for solution driven paper. More...
#include <secOrd_op_solutionDriven.h>
Classes | |
| struct | Data |
Public Member Functions | |
| Solution_driven (const Io::Parameter &, const Grid::Grid_and_time &, const Grid::Scal_FEfun &u_wrapper) | |
Get PDE parameter, time and growth promoting function 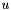 . More... . More... | |
| ~Solution_driven () | |
| Required for the pointer to implementation technique. | |
| void | solve (const Grid::Vec_FEfun &rhs, Grid::Vec_FEfun &lhs) const |
| Solve regularized mean curvature equation. More... | |
| void | brusselator_rhs (const Grid::Vec_FEfun &rhs, Grid::Vec_FEfun &lhs) const |
| Generates right-hand side without load vector for the linear system. More... | |
| void | operator() (const Grid::Vec_FEfun &rhs, Grid::Vec_FEfun &lhs) const |
| For debugging reasons. More... | |
Private Attributes | |
| std::unique_ptr< Data > | d_ptr |
| Pointer to data members. | |
Solve the surface partial differential equation for solution driven paper.
 for the surface equation, where
for the surface equation, where 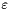 and
and 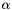 are small regularization parameter.
are small regularization parameter.
For given  search for
search for ![$X\colon \surface_{0} \times [0,T] \to \R^{m+1}$](form_13.png) such that
such that
![\begin{align*} v - \alpha \laplaceBeltrami v = {} & \parentheses[\big]{\varepsilon (-\meanCurvature) + \delta u} \surfaceNormal = \varepsilon \laplaceBeltrami X + \delta u \surfaceNormal, \\ \dell_{t} X = {} & v(X). \end{align*}](form_14.png)
For given  search for
search for  (surface nodal values) such that
(surface nodal values) such that
![\begin{equation*} \parentheses[\big]{M(X) + \alpha A(X)} \dell_t X = \varepsilon A(X)X + \delta M(u,\nodalValue{\surfaceNormal}) \end{equation*}](form_17.png)
For given 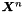 and
and 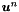 solve for
solve for 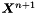
![\begin{equation*} \parentheses[\big]{M_3^n + (\alpha + \varepsilon\tau) A_3^n} \nodalValue{X}^{n+1} = (M_3^n + \alpha A_3^n) \nodalValue{X}^n + \tau \delta M_3^n(\nodalValue{u}^n, \nodalValue{\surfaceNormal}), \end{equation*}](form_21.png)
where 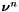 is elementwise normal.
is elementwise normal.
Definition at line 31 of file secOrd_op_solutionDriven.h.
| Solution_driven::Solution_driven | ( | const Io::Parameter & | p, |
| const Grid::Grid_and_time & | g, | ||
| const Grid::Scal_FEfun & | u_wrapper | ||
| ) |
Get PDE parameter, time and growth promoting function 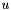 .
.
Extracts from Io::Parameter the parameter 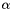 and
and 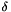 .
. Grid::Grid_and_time provides dynamical time steps via time_provider. More precisely we need the method velocity_regularization, surface_growthFactor and mcf_regularization from Io::Parameter.
u_wrapper outlive this object. Definition at line 67 of file secOrd_op_solutionDriven.cpp.
| void Solution_driven::brusselator_rhs | ( | const Grid::Vec_FEfun & | rhs, |
| Grid::Vec_FEfun & | lhs | ||
| ) | const |
Generates right-hand side without load vector for the linear system.
| rhs | 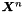 |
| lhs | 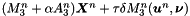 |
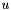 , which is given in the constructor, is still valid. The nodal values of
, which is given in the constructor, is still valid. The nodal values of rhs should be the nodes itself. Definition at line 84 of file secOrd_op_solutionDriven.cpp.
| void Solution_driven::operator() | ( | const Grid::Vec_FEfun & | rhs, |
| Grid::Vec_FEfun & | lhs | ||
| ) | const |
For debugging reasons.
| rhs | 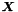 |
| lhs | 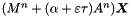 |
Definition at line 89 of file secOrd_op_solutionDriven.cpp.
| void Solution_driven::solve | ( | const Grid::Vec_FEfun & | rhs, |
| Grid::Vec_FEfun & | lhs | ||
| ) | const |
Solve regularized mean curvature equation.
| rhs | 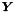 |
| lhs | Solution of ![$ \parentheses[\big]{M_3^n + (\alpha + \varepsilon\tau) A_3^n} \nodalValue{X}^{n+1} = \nodalValue{Y} $](form_27.png) |
rhs must be assembled. Definition at line 76 of file secOrd_op_solutionDriven.cpp.
 1.8.10
1.8.10