|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
|
Evolving surface finite element method
v0.3.0-14-g3598512
Numerical experiments for my papers
|
Standard heat resp. diffusion equation for an evolving or stationary surface problem. More...
Go to the source code of this file.
Classes | |
| class | Esfem::SecOrd_op::Linear_heat |
Namespaces | |
| Esfem | |
| The evolving surface finite element method. | |
| Esfem::SecOrd_op | |
| Parabolic and elliptic second order operators. | |
Standard heat resp. diffusion equation for an evolving or stationary surface problem.
Revised by Christian Power dd.mm.yyyy
Originally written by Christian Power
(power22c@gmail.com) 28. Januar 2016
Provides a class that performs the standard Dziuk Elliott evolving surface finite element discretization with implicit euler time discretization.
Search for  for
for
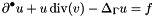
Search for  for
for
![\begin{equation*} \dell_t \parentheses[\big]{M(t) \nodalValue{u} } + A(t) \nodalValue{u} = M(t)\nodalValue{Pf}, \end{equation*}](form_3.png)
where 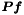 are the nodal values of the
are the nodal values of the 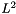 -projection of
-projection of 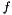 .
.
Given 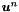 solve for
solve for 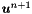
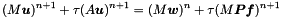
This programm implements a basic expression calculator. Input from cin; output to cout. The grammar for input is: etc.
Created by Christian Power on 28.01.2016 Copyright (c) 2016 Christian Power. All rights reserved.
Definition in file secOrd_op_linearHeat.h.
 1.8.10
1.8.10