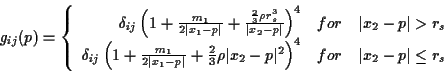Inverse Mean Curvature Flow (IMCF)

The motion of surfaces by their inverse mean curvature has been studied recently by Huisken and Ilmanen [HI]. Using this flow they were able to prove the Riemannian Penrose inequality of general relativity.

Here we present the results of our method for the numerical computation of the IMCF in asymptotic flat manifolds. The method itself together with some theoretical results can be found in [P], where one can also find some remarks on implementation issues.

The motion of a surface can be best experienced in movies. Therefore we have computed the following MPEG movies:

    Examples in Euclidean space


    Examples in other spaces


Resources for further information:

Deformation of a torus in Euclidean space

Suppose you start the IMCF with a thin torus in R3 with positive mean curvature. The torus will become thicker and the mean curvature approaches at some points zero. So the classical flow by inverse mean curvature, see [G] and [U], cannot exist for infinite time.
In the weak formulation of [HI] the surface will "jump" to its minimizing hull before this point is reached. The jump with infinite velocity occurs if the area of the surface would be larger than the area of its minimizing hull. After the jump the surface evolves in the classical fashion: in the rescaled limit it approaches the unit sphere.

In our example the large radius of the torus equals 2.0 and the small radius 0.5.

Movie (1591 kB)

Flow of two spheres in Euclidean space

For the weak formulation it doesn't matter if the starting surface is split into two ore more components. So in this example we start with to unit spheres. A classical solution for the IMCF exists up to the point where the two expanding spheres would touch. As in the last example the weak formulation jumps to the minimizing hull long before this point is reached.

Observe the catenoid that is formed as the connecting minimal surface between the two spheres.

Movie (1483 kB)

Two tori in Euclidean space

The last two examples can be combined: we start with two tori in Euclidean space and observe two topological changes of the initial surface. The first jump transforms the tori into discs, whereas the second one inserts a catenoid in between the
two discs.

Movie (504 kB)
 

Two spheres around two "black holes"

We use the following static metric, which is a modification of the classical static Schwarzschild metric:

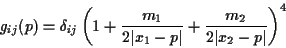
Both masses m1 and m2 are equal to one and x1=(2,0,0),  x2=(-2,0,0). The starting surface is composed out of two spheres of radius 0.55 around x1,  x2.

Movie (small screen size, 213 kB)
Movie (large screen size, 751 kB)

Sphere around "black hole" near a static star

Here we modify the conformal factor oft classical static Schwarzschild metric with the conformal factor of  the static metric of a star with constant density rho:

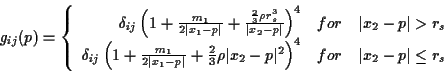
If the density rho is small (1.0) the flow is only a little perturbed:

Movie (small screen size, 422 kB), Movie (large screen size, 1093 kB),

but if the density is large (5.0) we see a jump over 3/4 of the star:

Movie (small screen size, 270 kB), Movie (large screen size, 930 kB)

References

Links

pasch@na.uni-tuebingen.de